Starcraft PGM rethink(WIP)

When I surf Kaggle dataset few years ago, I found a Starcraft “scouting” dataset. What can experts do using this dataset? Following related link, I found the paper [1].

Back to the time reading this paper, I don’t have enough knowledge to understand it. Recently I revisit the paper again and realize that I can give some ideas about this paper now.

The paper follow a classic PGM setting. I mean, it set some explicitly latent variables. The top is a HMM specifying “strategy”, that determine the production of units. Here’s the plate notation figure:

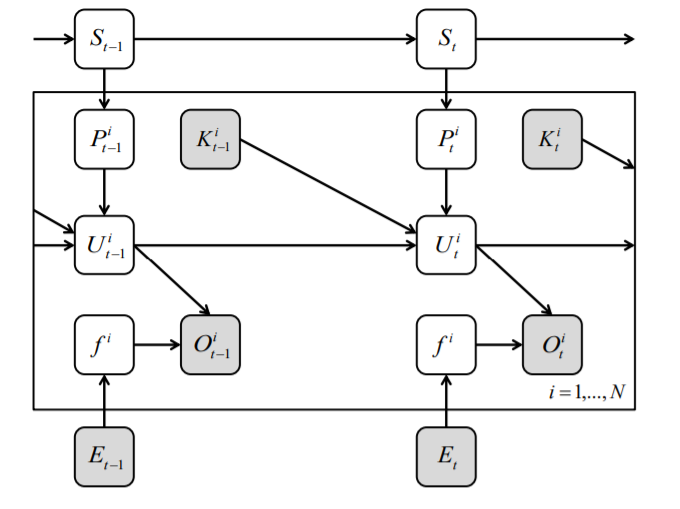
• $S$: Hidden strategy state.
• $P^i$: Produced type $i$ unit.
• $K^i$: Killed type $i$ unit.
• $U^i$: Current type $i$ unit.
• $O^i$: Observed type $i$ unit.
• $f^i$: A middle variable determined by $E$.
• $E$: Effort of scouting.

The gray plate denote observed variable, and other are latent variables.

The model is specified as:

Strategy model, a standard markov process:

$$\begin{align*} P(S_0) &\sim Multinomial(\eta_1,\dots,\eta_M) \\ P(S_t|S_{t-1} = s) &= Multinomial(\pi_1^s,\dots,\pi_M^s) \end{align*}$$

Production model:

$$P(P_t^i = k|S_t=s)=\begin{cases} 1 - \nu_s^i & k=0 \\ \nu_s^i \dot Pois(k-1;\lambda_s^i) & k>0 \end{cases}$$

Unexpected loss model:

$$\begin{align*} U_0^i &= c^i \\ U_t^i &\sim Binomial(U_{t-1}^i - K_{t-1}^i, 1-l^i) + P_t^i \end{align*}$$

Observation model:

$$\begin{align*} O_t^i &\sim BetaBinomial(U_t^i,\mu_t^i,\rho^i) \\ \mu, \rho &= f_\theta(E_t) \end{align*}$$

Learning

Now the model is fully specified, we should learn(fit) its parameters:

Parameters include $\mathbf{\eta}, \mathbf{\pi}, \mathbf{\nu}, \mathbf{l}, \mathbf{\theta}$ .Since $P$ is observed in training, usual learning method for HMM such as EM algorithm can be employed to estimate $\mathbf{\eta}, \mathbf{\pi}$.

Since $U$ is observed in training, we can fit $\mathbf{\theta}$ using any optimizing method with MLE can be used. denoting unobserved loss probability, denoted by $\mathbf{l}$, can be fitted using basic mean, given $U,f$.

HMM and EM algorithm learning

Let’s say we have a HMM:

$$P(z_0)\prod_{i=1}^N P(z_{n}|z_{n-1})P(x_n|z_n)$$

Inference

Now all of parameters are learned, we should do inference, the hardest part in many bayesian problems. The author use so called Rao-Blackwellised particle filtering(RBPF)[2] to infer the model.

Particle Filtering

Particle Filtering(PF), or Sequential Monte Carlo(SMC) use particle state with weight to approximate a distribution:

EM algorithm learning

Consider how to learn

Given observations $x_n$, we want get $P(z_{0:n}|x_{1:n})$. Following exact method, we get:

$$P(z_{0:N}|x_{1:N}) = \frac{P(x_{1:N}|z_{0:N})P(z_{0:N})} {\int_{z_{0:N}} P(x_{1:N}|z_{0:N})P(z_{0:N})} = \frac{P(z_0)\prod_{n=1}^N P(z_{n}|z_{n-1})P(x_n|z_n)} {\int_{z_0}P(z_0)\prod_{n=1}^N \int_{z_n} P(z_{n}|z_{n-1})P(x_n|z_n)}$$

When $z_n$ is discrete, $\int_{z_n} P(z_{n}

z_{n-1})P(x_n

z_n)}$ become a tractable form: $\sum_{z_n} P(z_{n}

z_{n-1})P(x_n

z_n)}$, while it’s not clear

References

1. Hostetler, Jesse, et al. “Inferring strategies from limited reconnaissance in real-time strategy games.” Proceedings of the Twenty-Eighth Conference on Uncertainty in Artificial Intelligence. AUAI Press, 2012.
2. Doucet, Arnaud, et al. “Rao-Blackwellised particle filtering for dynamic Bayesian networks.” Proceedings of the Sixteenth conference on Uncertainty in artificial intelligence. Morgan Kaufmann Publishers Inc., 2000.